Sistem Bilangan

SISTEM BILANGAN

(Bilangan Desimal, Biner, Oktal, dan HeksaDesimal)

 

1. BILANGAN DESIMAL

     Bilangan yang menggunakan 10 angka mulai dari 0 sampai 9 berturut turut. Setelah angka 9, maka angka berikutnya 10, 11, 12, dst.

     Contoh penulisan angka Desimal : 22_10, 5_10, 

Ingat, desimal berbasis 10, maka angka 10-lah yang menjadi Subscript pada penulisan Bilangan Desimal.

2. BILANGAN BINER

     Bilangan yang hanya menggunakan 2 angka, yaitu 0 dan 1. Bilangan Biner juga disebut bilangan berbais 2. Setiap bilangan pada bilangan biner disebut BIT. Dimana 1byte=8 bit.
     Contoh penulisan : 00111010_2, 10111010₂

3. BILANGAN OKTAL 

      Bilangan berbasis 8, yang menggunakan angka 0 sampai 7.

     _{Contoh penulisan : 178, 258}

_{4. BILANGAN HEKSADESIMAL}

 

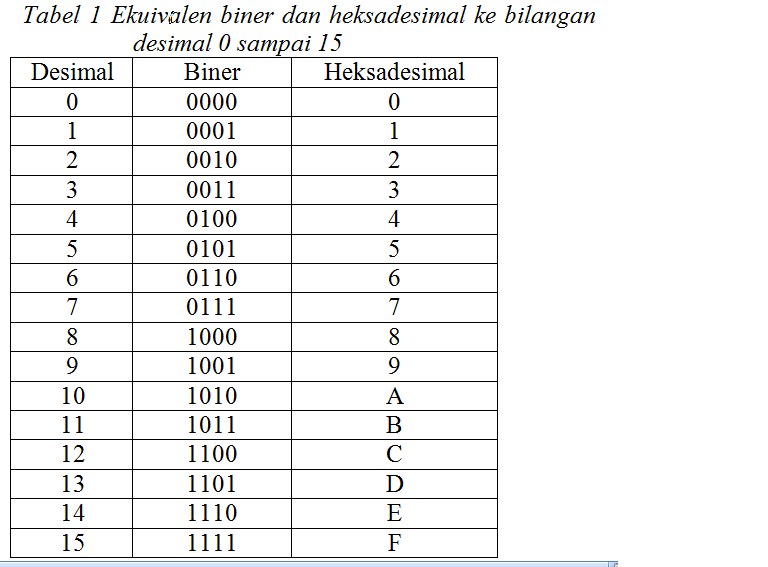
     _{Bilangan yang menggunakan 16 buah simbol, mulai dari 0 sampai 9, kemudian dilanjut dengan A sampai F yang merupakan simbol untuk 10 sampai 15.}

     _{Contoh penulisan : C516, B316}

SISTEM	RADIK
DESIMAL	10	0,1,2,3,4,5,6,7,8,9
BINER	2	0,1
OKTAL	8	0,1,2,3,4,5,6,7
HEKSADESIMAL	16	0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

   _{Radiks = Jumlah Digit}

_{KONVERSI BILANGAN}

     

_{1. Biner ke Desimal} 

  Untuk mengkonversi bilangan biner, kita harus memahami tabel dibawah ini:

128

64

32

16

8

4

2

1

     _{Dari gambar di atas, maka hasil dari 11111102 adalah 12610.}

_{2. Biner ke Oktal
     Untuk mengkonversi bilangan biner ke oktal, kita pisah tiap bilangan menjadi 3 digit dari belakang (kanan). Perhatikan tabel diii bawah ini:}

4

2

1

      Contoh soal: 11100112=. . . . . . . .8

_{1110011 = 001   110   011}

_{001 = 0+0+1     = 1}

_{110 = 4+2         = 6}

_{011 = 2+1         = 3}

                  _{Jadi = 1638}

_{3. Biner ke Heksadesimal}

 Untuk mengkonversi bilangan biner ke oktal, kita pisah tiap bilangan menjadi 4 digit dari belakang (kanan). Perhatikan tabel diii bawah ini:

8

4

2

1

       Contoh soal: 11111112=. . . . . . . .16

11100112 = 0111   0011 

0111 = 0+4+2+1 = 7

1111 = 8+4+2+1 = F

                   Jadi = 7F16

Sekian dulu yaa. . .  semoga bermanfaat. . . .  :)